こちらのページでは、音楽における「度数(ディグリー)」について詳しく解説していきます。
作曲や演奏に取り組んでいると、必ず「〇度」というような度数の表現に出会うはずです。
これから音楽理論を学んでいく際の基礎知識としても、是非これ以降の内容を参考にしてみて下さい。
目次
度数は「音の離れ具合」や「何番目か」を表す
音楽で扱われる「度数」とは、主に「二つの音の離れ具合(=音程)」を表すための言葉です。
いわゆる「角度」の表現と同じように、「1度」「2度」というような言い回しでこれを表します。
また、スケールやダイアトニックコードなどにおいて特定の音やコードが「何番目に位置するものか」ということを表す際にも、この「〇度」という言葉は使われます。
こちらの場合には、スケールの主音やダイアトニックコードの主和音を「1度」と捉え、「そこから数えて何番目か」ということを意味することが多いです。
一般的に語られる「度数」の概要
「角度」を表す際の度数には「0度」が存在し、それを起点とした二点の開き具合が大きくなるほど、度数は「1度、2度…」と増えていきます。
一方で、音楽における度数には「0度」が無く、「1度」を基準として数えます。
既にお伝えした通り、度数は主に「二つの音の離れ具合」を表す際に扱われるため、その差が無い場合(角度でいう「0度」)が「1度」となり、そこから音が離れるごとに「2度、3度…」と増えていきます。
以下は、音楽の度数でいう「1度(二つの音の差が無い状態)」を五線譜で表した図です。
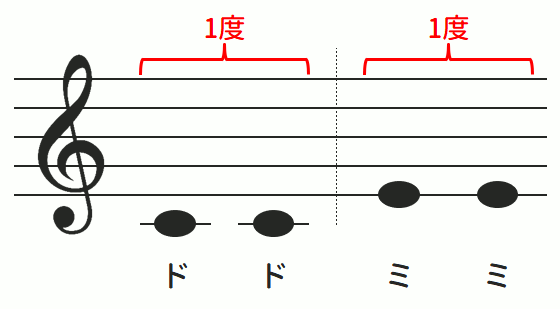
この例にある「ドとド」「ミとミ」は見ての通り同じ音であるため、それぞれは1度の関係となります。
度数を理解するうえで欠かせないのが、この「五線譜における二音の配置」をイメージする、ということです。
以下は、五線譜上に「2度」の関係になる音を表した図です。
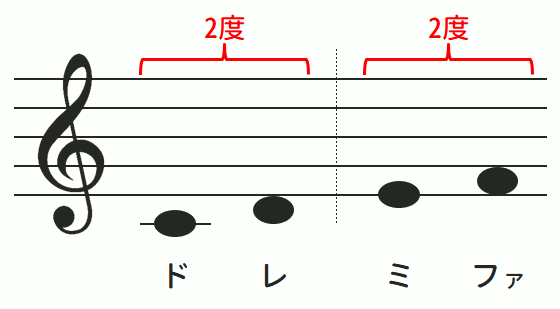
それぞれは五線譜上で1音だけ離れるように並べられた「ドとレ」「ミとファ」です。
これらは前述の「1度」に比べて二つの音の差が一段階広がっているため、「2度」という扱いとなります。
五線譜の線を数えると、二つの音が何度の関係になっているかがすぐにわかります。
1オクターブ内で「1度」から「7度」まで増える
前述したように、二音間の度数は五線譜における音の配置によって決まります。
そのため、例えば「ド」を起点とする場合に、度数は
- 「ド」と「ド」=1度
- 「ド」と「レ」=2度
- 「ド」と「ミ」=3度
- 「ド」と「ファ」=4度
- 「ド」と「ソ」=5度
- 「ド」と「ラ」=6度
- 「ド」と「シ」=7度
というように、「全7音ある『ド・レ・ミ・ファ・ソ・ラ・シ』内の音」との幅により「7度」まで増えます。
これは、その他の音を起点とする場合にも同じです。
すなわち、起点となる音ともう一つの音が隣り合っていればそれらの音程は「2度」、その間に音が一つ挟まって離れていれば「3度」…、というように言い表されるということを意味します。
以下はその例です。
ド・レ・ミ・ファ・ソ・ラ・シ
「ソとラ」
ド・レ・ミ・ファ・ソ・ラ・シ
ド・レ・ミ・ファ・ソ・ラ・シ
「ミとソ」
ド・レ・ミ・ファ・ソ・ラ・シ
上記例にあるように、例えば「ミ」と「ソ」の関係を度数で考えるときは、「ド・レ・ミ・ファ・ソ・ラ・シ」の並びに沿って「ミ(1)→ファ(2)→ソ(3)」と数え、「3度」とすぐに判別することができます。
同じ音名でも、高さによって度数が変わる
冒頭で述べた通り、度数は「二つの音がどれだけ離れているか」という点を言い表すものです。
そのため二つの音の音名が同じでも、どちらかの音の高さが変わることで度数も変わります。
以下はその例を示した図です。
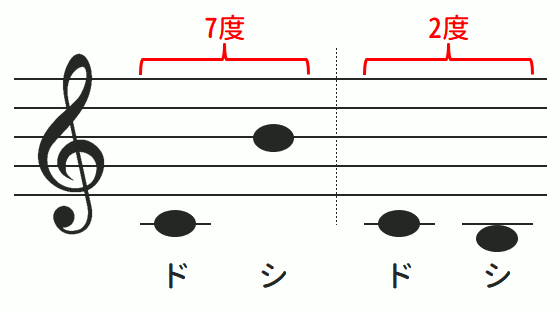
上記図は、それぞれ同じ音名を持つ「ド」と「シ」の度数の関係を表したものです。
図を見るとわかるように、「ド」から「高いシ」は間に「レ・ミ・ファ・ソ・ラ」を挟むため「ド(1)・レ(2)・ミ(3)・ファ(4)・ソ(5)・ラ(6)・シ(7)」で「7度」となり、一方で「ド」から「低いシ」は隣り合っているため「ド(1)・シ(2)」で「2度」となります。
これは、同じ「ドとシ」でもそれぞれがどう配置されているかによって度数は変わる、ということを意味します。
このように、度数は音名に紐づくのではなく、「二つの音の離れ具合=音程」に紐づくものだと理解しましょう。
1オクターブ以上離れている場合には「+7」
もちろん二つの音は1オクターブ以上離れることもあり、その場合に度数は前述の7度を通り越し「8度」以降の数を活用して表現されます。
以下はその例です。
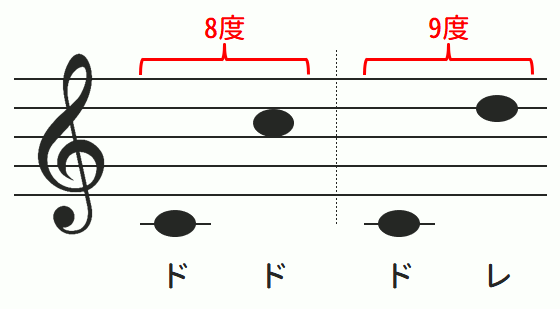
「ド」と「ド」は本来同じ音として「1度」と数えられますが、上記例の場合には間に1オクターブの隔たりがあるため「7度」を加えて「8度」となります。
また、同じように「ド」と「レ」は本来隣り合っており「2度」と数えられますが、この場合「2度」に「7度」を加えて「9度」となります。
このように、1オクターブ以上離れた音の関係を表す際には、通常の度数に「+7」をすることでその度数を求めることができます。
「スケール」や「ダイアトニックコード」の度数
冒頭で述べた「スケールやダイアトニックコードにおいて語られる度数」についても、基本的には上記を踏まえて活用されます。
スケールの度数
例えば、「ド・レ・ミ・ファ・ソ・ラ・シ」というメジャースケールがあった場合、主音の「ド」を「1度」として「ド(1)・レ(2)・ミ(3)」と数え、「ミは3度」というように捉えます。
これはキーが変わっても同じで、例えば
=「レ・ミ・ファ#・ソ・ラ・シ・ド#」
ポイントとなるのは「主音=1度」という存在で、スケールにおける度数の表現は主に「全体の中でどこに位置するか」という観点で語られることが多く、ほとんどの場合は主音を起点としつつ、全体を「ひとつの音の集まり」として捉えます。
すなわち、例えば「Cメジャースケール=ド・レ・ミ・ファ・ソ・ラ・シ」における「シ」はあくまでもひとつで、「ド・レ・ミ・ファ・ソ・ラ・シ」という枠の中で常に「7番目の音=7度」として語られる、ということです。
前述したように、「低いシ」という存在を意識して「ド(1)・シ(2)」と数えて「2度」とする、というようなことはあまりありません。
▼関連ページ
 メジャースケールの内容とその覚え方、割り出し方、なぜ必要なのか?について
メジャースケールの内容とその覚え方、割り出し方、なぜ必要なのか?について
ダイアトニックコードの度数
ダイアトニックコードにおいても、スケールとほぼ同じ観点で度数の表現が行われます。
ダイアトニックコードにおける主和音を「1度」と捉え、「何番目のコードか」ということを言い表すために度数が活用されます。
例えば、
=「C,Dm,Em,F,G,Am,Bm-5」
また、コード進行の構造のみを表す「度数(ディグリー)表記」もこれに付随するもので、一般的にダイアトニックコードは
主和音=1度(I)の存在がポイントとなるのも、スケールと同じです。
▼関連ページ
 ダイアトニックコードとスリーコード(概要や成り立ち、コードの役割などについて)
ダイアトニックコードとスリーコード(概要や成り立ち、コードの役割などについて)
さらに細分化される度数
「長い・短い」がある「2度」「3度」「6度」「7度」
ここで、改めて前述した「ドとレ」「ミとファ」の五線譜の図と、それを鍵盤の上に表した図を示します。

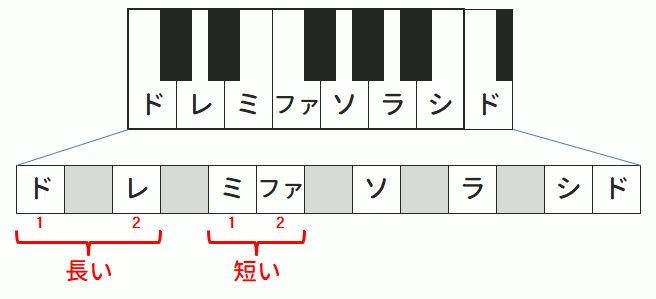
「ドとレ」「ミとファ」それぞれは五線譜上で同じ音の幅を持った「2度」でありながら、この図を見ると実際のところ「ド~レ」の方が長く、「ミ~ファ」の方が短い、ということがわかります。
このように、同じ度数でもそれを構成する音によって長さの種類が異なることがあります。
この例では、「長い2度」を「長2度(ちょうにど)」、「短い2度」を「短2度(たんにど)」と呼んでそれぞれを区別します。
また、上記と同じことが他に「3度」「6度」「7度」にもいえて、それぞれに「長・短」が存在します。
「1度」「4度」「5度」は完全
度数には残り「1度」「4度」「5度」が存在していますが、これらには「長・短」という概念がありません。
反面で、それらが変形したものを「増・減(ぞう・げん)」という言葉によって表現します。
以下はそれを把握するために、上記「2度」の例と同じように、「5度」の関係にあたる「シとファ」「ドとソ」を同じく図にしたものです。
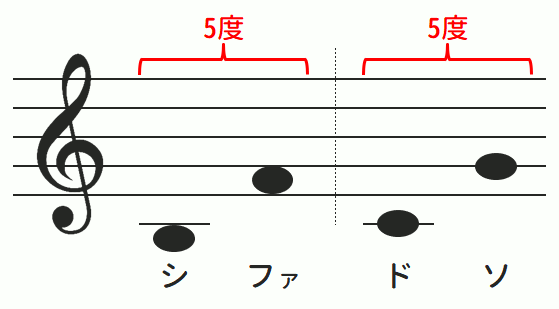
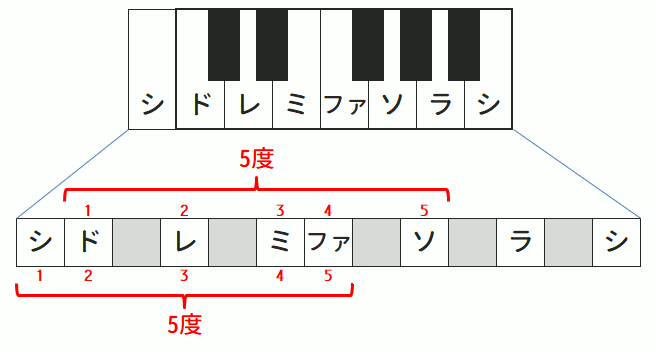
「シとファ」「ドとソ」のそれぞれは同じく「5度」という度数の関係になっていますが、上記鍵盤の図を見るとやはり双方の長さが異なっていることがわかります。
これを前述の例から「長5度・短5度」としたいところですが、この場合、より良く響く「ドとソ」を「完全5度(かんぜんごど)」と表現します。
そして、同じ5度でありながらあまり良い響きだと感じられない「シとファ」を「減5度(げんごど)」と表現します。
すなわち、より良く響く「1度」「4度」「5度」の音程を「完全」として、それが長くなったり短くなったりしたものを「増・減」として表現する、ということです。
「1~7度」の度数変化を整理する図
ここまでの内容を整理するために、楽典などにおいて度数を把握する際によく活用される図を以下に示します。
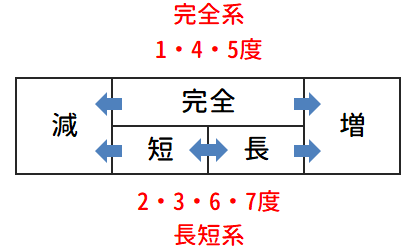
この図が表す内容は以下の通りです。
- 度数は「完全系(1・4・5度)」と「長短系(2・3・6・7度)」に分かれる
- 完全系は音程が広がると「増」、狭まると「減」と名前を変える
- 長短系は広い音程を持つものを「長」、狭い音程を持つものを「短」として区別する
- 長短系もさらに音程が広がったり狭まったりすることで「長・短」が「増・減」となる
ポイントとなるのは、度数が「完全系」と「長短系」という二種類に大きく分けられ、その前後に「増」「減」が存在している、ということです。
また、より厳密にはそのさらに先には「重増」「重減」という音程も存在していますが、ポップス・ロックにおいてそのあたりの概念はあまり活用されません。
まとめ
ここまで度数について詳しく解説してきました。
説明を改めてまとめると、以下のようになります。
- 度数は「二つの音の離れ具合=音程」を表す
- スケールやダイアトニックコードにおいては、「全体の中で何番目か」ということを表すために度数が活用される
- 「1度」から始まり、オクターブ内で音が離れるごとに「7度」まで増える
- 同じ度数でも音の関係によってさらに「長短」「増減」などと細分化される
- 度数は「完全系(1・4・5度)」と「長短系(2・3・6・7度)」に分かれる
- 1オクターブ以上の音程は「+7」により「8度」以上の数字を使って表現される
ポップス・ロックの作曲において、度数はコードの構成音を考えたり、スケールやダイアトニックコード内の音やコードの動きを把握するために活用します。
実際に五線譜や鍵盤を活用しながら、それぞれの音と音程、度数の関係を改めて整理してみて下さい。


 著者:
著者:


