コード進行を表現する時に
I→VI→II→V(1→6→2→5)
などの数字が扱われているのを目にすることがあるはずです。
これを「度数(ディグリー)表記」などと呼びますが、こちらでは
- そこで扱われている数字の意味
- なぜそのような表記をするのか?
- 代表的な数字の組み合わせ(パターン)
などについて詳しく解説します。
コード進行で使われる数字の意味
既に述べた通り、コード進行の成り立ちを示したり、それらを柔軟に扱う際には
- 1→6→2→5
- 4→5→3→6
というように、数字を使って表記するのが一般的です。
多くの場合、度数表記には、「I」「II」のようなローマ数字が用いられます
この数字は
「ダイアトニックコード」におけるコードの場所(役割/度数)
を意味しており、これを理解するためには、
- キー
- 度数
- ダイアトニックコード
という三つの概念について簡単に把握しておく必要があります。
▼それぞれについて、詳しくは以下のページでも解説しています。
 キー(音楽)について キー=「中心音」と「まとまりのある音のグループ」を意味する言葉
キー(音楽)について キー=「中心音」と「まとまりのある音のグループ」を意味する言葉
 音楽における「度数(ディグリー)」の詳細について(音程や「何番目か」を表す「度」という概念)
音楽における「度数(ディグリー)」の詳細について(音程や「何番目か」を表す「度」という概念)
 ダイアトニックコードとスリーコード 概要や成り立ち、コードの役割などについて
ダイアトニックコードとスリーコード 概要や成り立ち、コードの役割などについて
「キー」「度数」という概念
上記で挙げた解説ページでも述べている通り、そもそも音楽には「キー」という考え方があり、それによって曲の中で主に扱う音をある程度定めたうえで曲が組み立てられます。
以下は、キー別に「主に扱う音」を一覧にした表です。
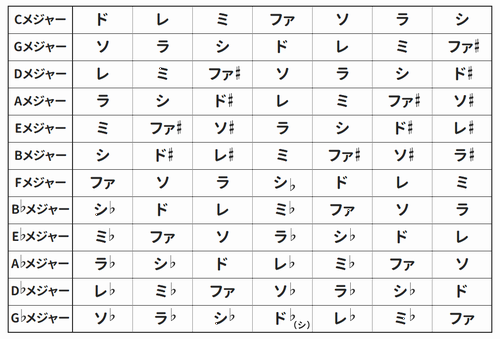
この表にある通り、例えば「キー=Cメジャー」や「キー=Dメジャー」という場合、それぞれの音楽では
- 【キー=Cメジャー】ド・レ・ミ・ファ・ソ・ラ・シ
- 【キー=Dメジャー】レ・ミ・ファ#・ソ・ラ・シ・ド#
という7音がその曲で主に扱われることになります。
音には全部で12個の種類しかありませんが、それらをやみくもに使うと音楽がぐちゃぐちゃになってしまうため、「キー」という概念によって「主に扱う音」を7個定めることでまとまりを感じられるようになります。
この時の
- 【キー=Cメジャー】・・・ド
- 【キー=Dメジャー】・・・レ
を「主音」と呼び、これらは別の言い方をすれば「中心音」として、キーにおける音使いの中心的な役割を担います。
そのうえで、音楽では「主音」を「1度」と捉え、全7音を「1度~7度」で表現します。
これが「度数」による表記であり、つまり「キー=Cメジャー」においては
- ド=1度
- レ=2度
- ミ=3度
- ファ=4度
- ソ=5度
- ラ=6度
- シ=7度
と表現する、ということです。
本来の「度数」は音程を表すために使う単位ですが、「キーの音使い」を考える際には中心音を「1度」とするため、必然的にそこから7度までの音が存在することになります。
コード進行も「キー」の中に成り立つもの
ここで話をこのページのテーマである「コード進行」に戻すと、通常それらも前述の「キー」の概念に沿って組み立てられます。
上記の例を流用すれば、同じように
- 【キー=Cメジャー】ド・レ・ミ・ファ・ソ・ラ・シ
- 【キー=Dメジャー】レ・ミ・ファ#・ソ・ラ・シ・ド#
が、それぞれのキーにおける「主に使われるコード」や、それをつなげた「コード進行」になるのです。
例えば「キー=Cメジャー」という場合、
ド・レ・ミ・ファ・ソ・ラ・シ
の7音それぞれを土台(ルート音)として、そこからそれらの音を3度ずつ積み上げるように重ねます。
それによって
- ド・ミ・ソ=「C」
- レ・ファ・ラ=「Dm」
- ミ・ソ・シ=「Em」
- ファ・ラ・ド=「F」
- ソ・シ・レ=「G」
- ラ・ド・ミ=「Am」
- シ・レ・ファ=「Bm-5」
という7個のコードができあがります。
上記を見るとわかる通り、ここではそれぞれのコードが「ド・レ・ミ・ファ・ソ・ラ・シ」の音のみによって成り立っています。
このような概念によってできあがったコードのグループを「ダイアトニックコード」と呼び、前述した「キーの音」と同じく、音楽ではこれらが「キーのコード」となります。
以下は、それぞれのキーにおけるダイアトニックコードを一覧にした表です。

そして、既に述べた「度数」の概念がここでも活用され、例えば「キー=Cメジャー」においては
- ド・ミ・ソ=「C」を「1度(I)」
- レ・ファ・ラ=「Dm」を「2度(II)」
のように言い表します。
数字(度数)をダイアトニックコードに当てはめる
ここで、さらに話をこのページの中心的なテーマである「コード進行の数字」に戻すと、例えばページ冒頭でご紹介した
1→6→2→5
という数字の連なりは、既に述べた通り「ダイアトニックコード」におけるコードの場所を度数によって表記したものだということが理解できます。
つまり、上記は
1度→6度→2度→5度
を意味しており、それを前述した「ダイアトニックコード一覧」に当てはめれば、例えば「キー=Cメジャー」の場合
C→Am→Dm→G
というコード進行に置き換えることができます。
このように、「コード進行を数字で表したものは何を意味しているか?」と考えるときには、まずキーの「ダイアトニックコード」と、その中にある「1度」から「7度」までのコードを思い出し、それらのつながりを度数によって表記したもの、と理解して下さい。
構造が変わらないため数字(度数)で把握できる
では、なぜこのように「数字による表記」が一般的になっているかといえば、そこには
キーが変わっても構造は変わらない
という音楽の特性があるからです。
キーが変わっても、構造は同じ
これを理解するために、上記でご紹介した「キーの音一覧」の表から、「キー=Cメジャー」「キー=Dメジャー」の音を改めて抜き出し、それを鍵盤の図と共に並べたものを以下に示します。
- 【キー=Cメジャー】ド・レ・ミ・ファ・ソ・ラ・シ
- 【キー=Dメジャー】レ・ミ・ファ#・ソ・ラ・シ・ド#
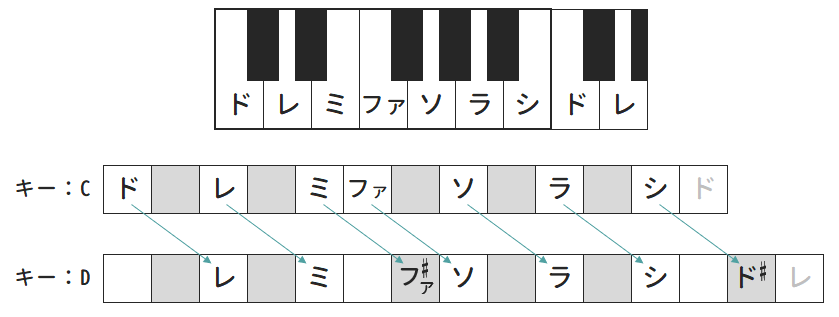
この図を見るとわかるとおり、
ド・レ・ミ・ファ・ソ・ラ・シ
と
レ・ミ・ファ#・ソ・ラ・シ・ド#
は、中心音が「ド」と「レ」というように違っているだけで、全7音の並び具合(間隔)が同じです。
つまり、「レ・ミ・ファ#・ソ・ラ・シ・ド#」は、
「ド・レ・ミ・ファ・ソ・ラ・シ」の音階の感じを「レ」を中心として表現したもの
と定義できます。
この概念は、正確には「メジャースケール」と呼ばれるものです。
▼関連ページ
 メジャースケールの内容とその覚え方、割り出し方、なぜ必要なのか?について
メジャースケールの内容とその覚え方、割り出し方、なぜ必要なのか?について
ダイアトニックコードも各キーで同じ構造を持つ
この構造は、ダイアトニックコードにももちろん引き継がれます。
すなわち、例えば
- 「キー=Cメジャー」のダイアトニックコード
- 「キー=Dメジャー」のダイアトニックコード
を考える場合、それぞれが「同じ構造をもった7個の音」から成り立っているため、できあがるコードも同じ構造になる、ということを意味します。
以下の表は、前述した「ダイアトニックコード一覧」の表から「キー=Cメジャー」「キー=Dメジャー」それぞれのダイアトニックコードを抜き出したものです。

これを見ると、例えば
- 1度、4度、5度のコードはそれぞれアルファベットのみ
- 2度、3度、6度のコードはそれぞれアルファベットに「m」が併記されている
- 7度のコードはさらにそれぞれ「-5」が併記されている
というように、それぞれのキーのコードが同じ構造を持っているとわかります。
数字表記によって構造による把握ができる
それぞれのキーが同じ構造を持つ、という点は、
コード進行を構造によって把握しておけば、それをさまざまなキーに置き換えることができる
という、作曲や演奏における利点にそのままつながります。
例えば前述の
1→6→2→5
は、「キー=Cメジャー」で表現すれば
C→Am→Dm→G
であり、これを「キー=Dメジャー」で表現すれば
D→Bm→Em→A
となります。
つまり、この「1→6→2→5」のような数字による度数表記が「コード進行の型」のようなものとして活用できて、その型を利用することでそれぞれのキーにおいて瞬時に目的とするコード進行を作り上げることができるのです。
実際のところ、コード進行を数字(度数)で表す理由は他にもいくつかありますが、根本的にはこのような理由によって度数表記が活用されていると理解して下さい。
代表的な数字パターン(コード進行の定型)
これ以降は、コード進行の数字(度数)表記による代表的なパターンをいくつかご紹介します。
【1】1→4→5→6(I→IV→V→VIm)
まず、コード進行の数字表記を考えるうえで最も典型的なのが、この「1→4→5」に関連する形です。
これは、ダイアトニックコードにおける主要三和音=スリーコードを活用したコード進行で、それら三つのコードは三種の機能を代表するものとされています。
通常、ここでの「5」に相当するダイアトニックコード内の5度のコード(V)は「ドミナント」という不安定な響きを持つため、そこから最も安定した響きを持つ1度(I)につながります。
ここでは、「1→4→5→6」とし、それを少し裏切るような形を作っていますが、これは「偽終止」と呼ばれるものです。
▼関連ページ
 ダイアトニックコードとスリーコード 概要や成り立ち、コードの役割などについて
ダイアトニックコードとスリーコード 概要や成り立ち、コードの役割などについて
 終止の詳細とその種類(全終止・偽終止・アーメン終止・サブドミナントマイナー終止など)
終止の詳細とその種類(全終止・偽終止・アーメン終止・サブドミナントマイナー終止など)
【2】1→6→2→5(I→VIm→IIm→V)
次にご紹介するのが、前述したスリーコードの構成をややクラシカルにアレンジした「1→6→2→5」の形です。
この形は「循環コード」とも呼ばれるもので、ループの構成やセッションなどで頻繁に活用されます。
スリーコードと同じく三種の機能が盛り込まれており、トニック→サブドミナント→ドミナント、というスムーズな流れを生み出しているところがその特徴だといえます。
▼関連ページ
 循環コードの詳細と成り立ち・派生形や「逆循環コード」についての解説など
循環コードの詳細と成り立ち・派生形や「逆循環コード」についての解説など
 ツーファイブとは?(概要と基本的な成り立ち、活用方法、マイナーキーにおける例など)
ツーファイブとは?(概要と基本的な成り立ち、活用方法、マイナーキーにおける例など)
【3】3→6→2→5(IIIm→VIm→IIm→V)
上記「1→6→2→5」を少しアレンジしたのが、この「3→6→2→5」です。
冒頭の「1度(I)」のコードを「3度(III)」に差し替えているだけですが、マイナーコードが増える分、やや切ない響きが強まります。
【4】4→5→3→6(IV→V→IIIm→VIm)
ダイアトニックコードを活用したコード進行の中でも、少し特徴的なのがこの「4→5→3→6」です。
ここでは4度(IV)をコード進行の冒頭に置いていますが、これはサブドミナント(一時不安)と呼ばれる機能を持つコードで、トニックとはまた違ったどっちつかずな響きを持っています。
このコード進行は前述した「3→6→2→5」と同じく「1度」のコードが含まれておらず、そのキーの中心的なコード(主和音)が登場しないという意味でもあやふやな雰囲気を持つコード進行だといえます。
▼関連ページ
 「4536進行」(コード進行の代表的な形)についての解説|その詳細と活用される理由、アレンジ型など
「4536進行」(コード進行の代表的な形)についての解説|その詳細と活用される理由、アレンジ型など
【5】6→4→5→1(VIm→IV→V→I)
マイナーコードで始まりメジャーコードで締めくくる形として、この「6→4→5→1」の形も有名です。
こちらに含まれる「VIm」および「I」は共にトニックの機能を持つため、コード進行全体の安定感が保たれている点もこのコード進行が好まれる点だといえます。
この構成は、小室哲哉さんが愛用していることから「小室進行」などとも呼ばれます。
前述した「1→6→2→5」とはまた違った意味で、何度も繰り返して演奏されることが多いです。
▼関連ページ
 「6451」型のコード進行の解説(通称:小室進行) 親しみやすさの考察と既存曲の例
「6451」型のコード進行の解説(通称:小室進行) 親しみやすさの考察と既存曲の例
まとめ:コード進行を数字(度数)=構造で把握することの効果
コード進行の数字(度数)表記について、以前に以下の投稿をしました。
これよく言いますが、コード進行を上手に作れるようになるための練習に「コード譜の度数読み」をおすすめします。知っている曲のコード譜を見て、キーを明らかにしたうえですべてのコードを度数で解釈していくとコード進行の構造が見えてくる。構造がわかれば自分でもそれを作れるようになります。
— うちやま|作曲の先生 (@sakkyoku_info) August 21, 2022
この投稿で述べている通り、コード進行の数字(度数)表記は、
- コード進行を構造によって把握できる
- 数字のパターンによってコード進行の型を覚えやすい
- 構造=コード進行の型によっていろいろなキーに対応できる
などの利点につながります。
現在「コード進行がうまく作れない」と悩んでいる人は、この数字表記を活用しながら、是非「コードの流れを構造で把握すること」に取り組んでみて下さい。
全体を広い視点によって捉えることで分析力が強化され、柔軟な発想でコード進行を作り上げていくことができるようになるはずです。

音楽理論について詳しく知る
 音楽理論を知りたい人のための「学習の見取り図」※独学に活用できる「音楽理論の何をどの順番で学べばいいか」のまとめ
音楽理論を知りたい人のための「学習の見取り図」※独学に活用できる「音楽理論の何をどの順番で学べばいいか」のまとめ
ポップス・ロック作曲の上達につながる「曲分析ガイドブック」について知る
 作曲がぐんぐん上達する「曲分析ガイドブック」のご紹介
作曲がぐんぐん上達する「曲分析ガイドブック」のご紹介

 著者:
著者: