サークルオブフィフス（サイクルオブフィフス・五度圏）の解説 詳細とコード進行等への活用方法について

ポピュラー系の音楽理論を学んでいると「サークルオブフィフス」（サイクルオブフィフス・五度圏）という言葉をよく耳にするはずです。

サークルオブフィフスは音楽理論の学習やコード進行の組み立てに活用できる概念で、これを知っておくと音同士の関係を簡単に把握することができるようになります。

こちらのページではそんな「サークルオブフィフス」の詳細と、主にコード進行等への活用方法について解説していきます。

「サークルオブフィフス」の概要

「サークルオブフィフス」とは、日本語で「五度圏」と訳されるように、「音を5度の音程でつないで輪にした図」のことを指す言葉です。

以下はサークルオブフィフスの図です。

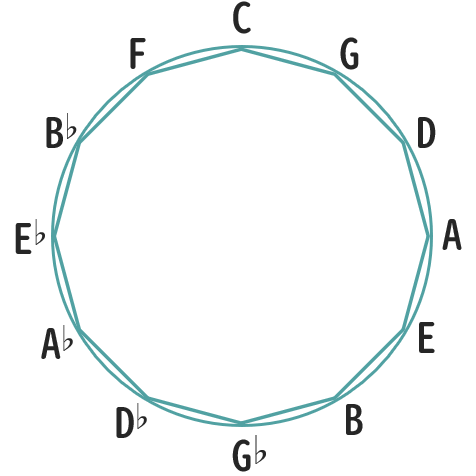
輪のまわりに12個のアルファベットが並んでいますが、これは音として存在する全12音を指すものです。

この図における音の並び方を理解するためには、「音程」や「度」という概念について知っておく必要があります。

「完全5度」の音程について

そもそも、二つの音の高さの差（音程）は「度」という言葉で言い表されます。

▼関連ページ
音楽における「度数（ディグリー）」の詳細について（音程や「何番目か」を表す「度」という概念）

それぞれは音程の違いによって「1度」「2度」…というように表現され、中でもメジャースケールにおける「主音」と「属音」の関係にあたる「完全5度」の音程は重要なものとされています。

以下はその例として、「Cメジャースケール（ド・レ・ミ・ファ・ソ・ラ・シ）」における主音「ド」と属音「ソ」の関係＝完全5度を図にしたものです。

この図を見るとわかるように、完全5度の音程は

として定義できます。

完全5度をつなげて輪にする

話を「サークルオブフィフス」に戻すと、それは既に述べた通り、音を「完全5度」の音程でつなげて輪にすることで成り立っています。

つまり、前述した「ド→ソ」という完全5度の音程を再度完全5度によって「ソ→？」と次につなげ、それを何度も続けることで音を連ねて「輪・環状（リング）」のような形を作っている、ということです。

以下は、「ド→ソ」という完全5度音程から、その続きである「ソ→レ」「レ→ラ」の完全5度音程を表した図です。

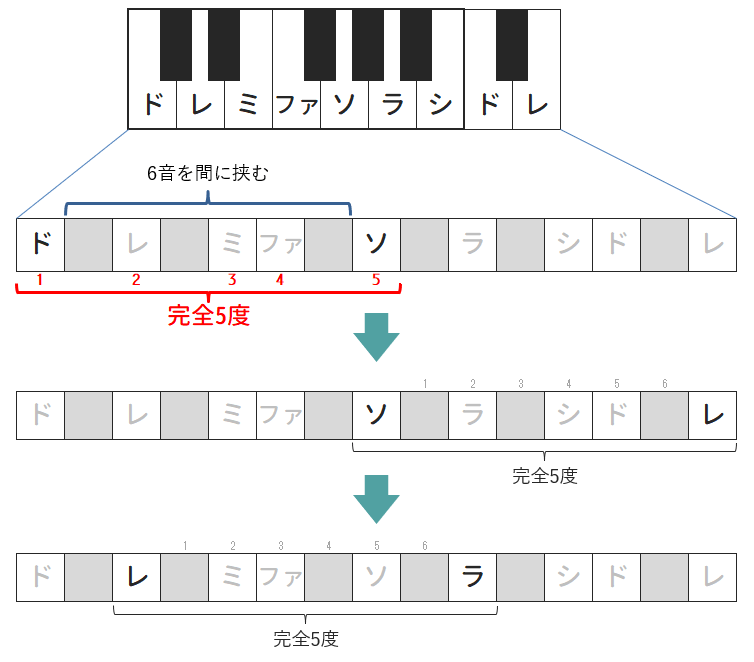
この図にある通り、完全5度によって音は

• ド→ソ
• ソ→レ
• レ→ラ

とつながっていきますが、これをさらに先へ続けると音は

• ラ→ミ
• ミ→シ
• シ→ソ♭
• ソ♭→レ♭
• レ♭→ラ♭
• ラ♭→ミ♭
• ミ♭→シ♭
• シ♭→ファ
• ファ→ド

という形で発展し、最終的に「ド」に戻ってくることができます。

以下に改めてサークルオブフィフスの図を示します。

この輪のまわりに書かれたアルファベットはそのようなことを意味しており、時計回りに書かれた

という表記は、前述の「ド→ソ」「ソ→レ」…をアルファベットで表したものです。

「サークルオブフィフス」の活用方法

ここまでを通して「サークルオブフィフス」の成り立ちがわかったところで、

• これが何の役に立つの？
• 「サークルオブフィフス」をどう活用すればいいの？

という疑問がわきます。

ページ冒頭で述べた通り、「サークルオブフィフス」は音同士の関係を簡単に把握したり、コード進行を組み立てたりするのに活用できます。

以下に、その具体的な活用方法を挙げます。

「完全5度下」への強進行を把握する

まず、「サークルオブフィフス」は完全5度によって音をつなげて輪にしたものであるため、それに関連する音やコードの動きを作ったり、それらを把握したりする際に活用できます。

「完全5度」で真っ先に思いつくのが「強進行」です。

▼関連ページ
強進行について（通称「4度進行」＝ドミナントモーションの元になる力強い音の動き）

「強進行」とは「強いつながりを感じさせる音の動き」を指す言葉です。

いくつかあるその動きの中でも最も強いとされているのが、まさに「サークルオブフィフス」で扱われている「完全5度」の動きです。

前述の例で挙げた

• ド→ソ
• ソ→レ
• レ→ラ …

などは、完全5度を「低い音から高い音」に向けて進めるように作っていましたが、これを逆にした

• ソ→ド
• レ→ソ
• ラ→レ …

などがここでの「強進行」にあたります。

これをここでは「完全5度下」と言い表しますが、つまり「サークルオブフィフス」にある音を反時計回りに動かすことでこの「完全5度下」の音の動きを簡単に把握することができるのです（以下図）。

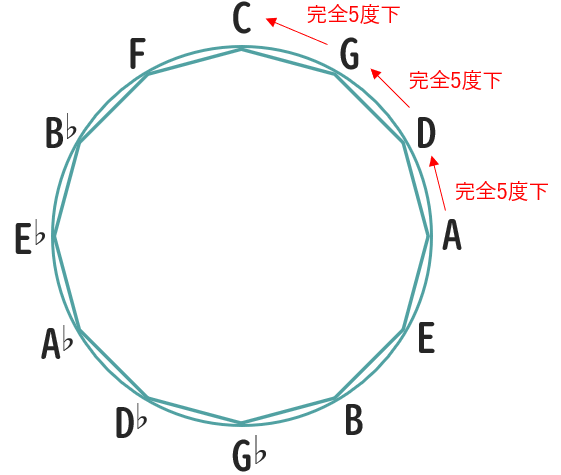
この図にある通り、例えば「A→D（ラ→レ）」が強進行であり、そこからつながる「D→G（レ→ソ）」「G→C（ソ→ド）」も同じだとすぐに把握できます。

強進行となるコード進行を把握する

上記の「完全5度」の強進行は、それをコードのルート音に置き換えることでそのままコード進行にも流用することができます。

すなわち、上記で図として表した

• 「A→D」
• 「D→G」
• 「G→C」

などの完全5度下への音の動きを、そのまま

• 「Am7→D7」
• 「D7→G」
• 「G→Cm」

などのコード進行に置き換え、スムーズなコードの流れを作り出すことができる、ということです。

「ツーファイブワン」を把握する

コードには

• 安定（トニック）
• 不安定（ドミナント）
• 一時不安（サブドミナント）

という三種の機能があり、それらがコンパクトな形で結びついた「ツーファイブワン」というコード進行の型は、ポピュラー音楽のコード進行を考えるうえで基本となるものです。

▼関連ページ
ツーファイブとは？（概要と基本的な成り立ち、活用方法、マイナーキーにおける例など）

詳しい解説は上記ページに譲りますが、この「ツーファイブワン」は

というような型に沿って、上記で述べた「完全5度下」でコードを連ねて作り出すことができます。

つまり、同じようにサークルオブフィフスを活用できるのです。

以下は、その例としていくつかの「ツーファイブワン」をサークルオブフィフスを活用して作ったものです。

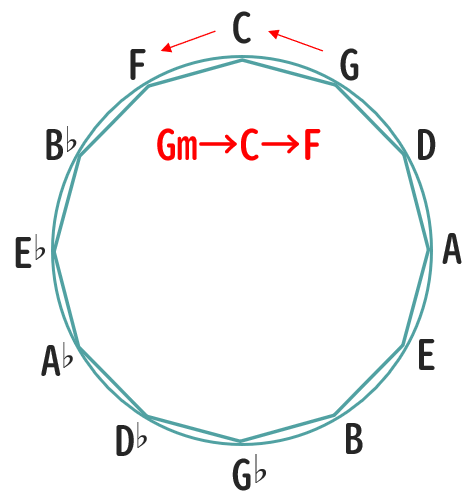
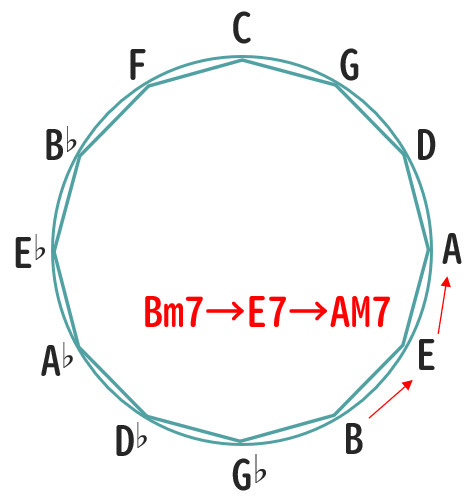
ここから、サークルオブフィフスの図を手元に置いておけば、それをそのままコードに置き換えてスムーズな「ツーファイブワン」のつながりを作り上げていけることがわかります。

また、例えば既存のコード譜から

のようなコードのつながりを見つけた場合、

という観点からサークルオブフィフスとそれを照らし合わせ、確認することもできます。

「ドミナントセブンス」を把握する

ここまでに述べている「完全5度下」へのコードの動きは、ツーファイブワンにも含まれているように「V7→I」「V7→Im」として解釈できます。

そこから

と考えるときにもサークルオブフィフスが活用できます。

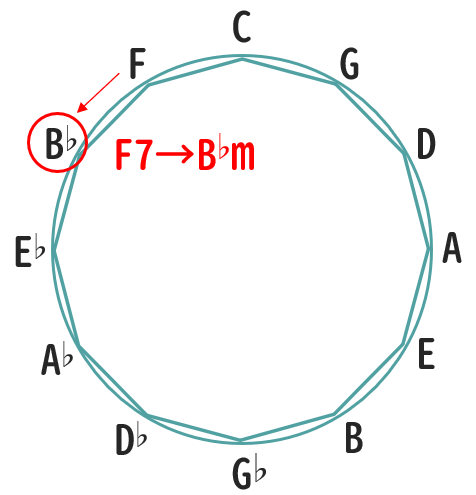
例えば「B♭m」というコードがあった場合、それに対するドミナントセブンス（V7）が何かを考えるときにはサークルオブフィフスを見て「完全5度下」の動きから瞬時に「F7」というコードが導けます（以下図）。

「スリーコード」を把握する

サークルオブフィフスで隣り合う三つのコードは、ダイアトニックコードにおける「I」「IV」「V」と同じものです。

以下は、その例として「キー＝C」「キー＝E」のダイアトニックコードを示したものです。

そのうえで、サークルオブフィフスを確認してみると、三つのコードがそれぞれ隣り合っていることがわかります（以下図）。

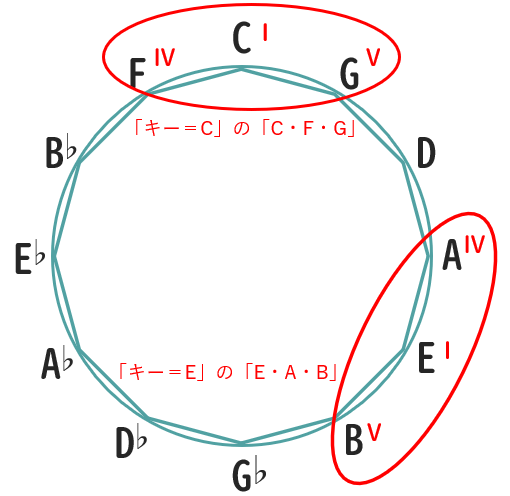
この「I」「IV」「V」は「スリーコード」と呼ばれ、前述した「コードの機能」を象徴するものです。

このように、スリーコードを活用したコード進行もサークルオブフィフスを使うことで簡単に作り上げることができます。

▼関連ページ
ダイアトニックコードとスリーコード　概要や成り立ち、コードの役割などについて

「裏コード」を把握する

上記で述べた「ドミナントセブンス（V7）」には、「置換ドミナント」と呼ばれるコードが存在しています。

これは通称「裏コード」と呼ばれるもので、具体的には「♭II7」のことを指します。

▼関連ページ
裏コードについて ドミナントコードの代理ができるコードを解説

上記ページで述べているように、例えば「キー＝C」においてそれらは

• V7＝G7
• ♭II7＝D♭7

のような関係となりますが、例として

というコード進行を、裏コードを使うことで

のようにアレンジすることができます。

サークルオブフィフスはこの裏コードを把握するのにも活用できて、具体的には輪の中で向かい合った位置に裏コードが存在しています。

以下は、上記で述べた「G7」の裏コード「D♭7」を割りだした図です。

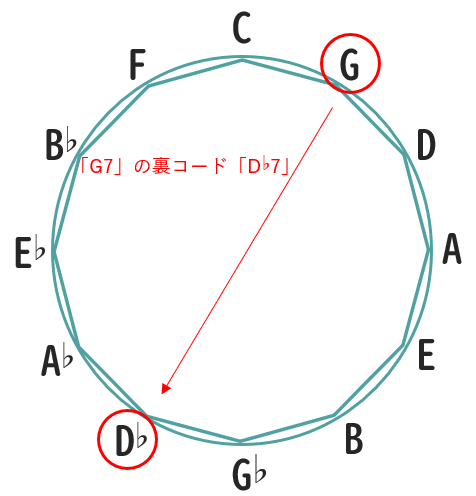
「G」に向かい合う形で「D♭」が存在しているため、ここから「G7」に対する裏コードは「D♭7」である、と簡単に導くことができます。

まとめ

ここまで、「サークルオブフィフス」の詳細とその活用方法について解説してきました。

上記にとどまらず、「サークルオブフィフス」はさまざまな観点から活用されており、特にポップス・ロックの作曲においてスムーズなコードのつながりを作り上げたり、コード進行を分析したりするのに役立てられています。

この図を手元に置いておき、積極的に使用することでその使い勝手を体感してみて下さい。

音楽理論について詳しく知る

音楽理論を知りたい人のための「学習の見取り図」※独学に活用できる「音楽理論の何をどの順番で学べばいいか」のまとめ

ポップス・ロック作曲の上達につながる「曲分析ガイドブック」について知る

作曲がぐんぐん上達する「曲分析ガイドブック」のご紹介ページ